시험범위가 전범위라 이번학기 배운 전체 내용에 대해 급하게 정리한다.

Classifier

Decision Tree

• 결정 트리 학습법(decision tree learning)은 어떤 항목에 대한 관측값과 목표값을 연결시켜주는 예측 모델로써 결정 트리를 사용한다

  장점

• 결과를 해석하고 이해하기 쉽다.간략한 설명만으로 결정 트리를 이해하는 것이 가능하다.
• 자료를 가공할 필요가 거의 없다.다른 기법들의 경우 자료를 정규화하거나 임의의 변수를 생성하거나 값이 없는 변수를 제거해야 하는 경우가 있다.
• 수치 자료와 범주 자료 모두에 적용할 수 있다.다른 기법들은 일반적으로 오직 한 종류의 변수를 갖는 데이터 셋을 분석하는 것에 특화되어 있다. (일례로 신경망 학습은 숫자로 표현된 변수만을 다룰 수 있는 것에 반해 관계식(relation rules)은 오직 명목 변수만을 다룰 수 있다.
• 화이트박스 모델을 사용한다. 모델에서 주어진 상황이 관측 가능하다면 불 논리를 이용하여 조건에 대해 쉽게 설명할 수 있다. (결과에 대한 설명을 이해하기 어렵기 때문에 인공신경망은 대표적인 블랙 박스 모델이다.)
• 안정적이다. 해당 모델 추리의 기반이 되는 명제가 다소 손상되었더라도 잘 동작한다.
• 대규모의 데이터 셋에서도 잘 동작한다. 방대한 분량의 데이터를 일반적인 컴퓨터 환경에서 합리적인 시간 안에 분석할 수 있다.

  단점

• 최적의 결정 트리를 학습하는 문제는 NP-완전 문제로 알려져 있고, 이는 최적화의 관점에서나 아니면 더 간단한 개념의 측면에서도 마찬가지이다. 결과적으로, 실질적인 결정 트리 학습 알고리즘은 각 노드에서의 부분 최적값을 찾아내는 탐욕 알고리즘 같은 휴리스틱 기법을 기반으로 하고 있다. 이런 알고리즘들은 최적 결정 트리를 알아낸다고 보장할 수는 없다. 부분 최적화에 의한 영향을 줄이기 위하여 이중 정보 거리(dual information distance, DID)와 같은 방법을 사용하기도 한다.
• 결정 트리 학습자가 훈련 데이터를 제대로 일반화하지 못할 경우 너무 복잡한 결정 트리를 만들 수 있다. (이를 과적합 문제라 한다.) 이 문제를 해결하기 위해서 가지치기 같은 방법을 사용하여야 한다.
• 결정 트리로는 배타적 논리합이나 패리티, 멀티플렉서와 같은 문제를 학습하기 어렵다. 이런 문제를 학습하기 위해서는 결정 트리가 엄청나게 커지기 때문에 문제의 표현 방법을 바꾸거나 통계 관련 학습법이나 귀납 논리 프로그래밍처럼 더 많은 것을 표현할 수 있는 학습 알고리즘을 사용하여야 한다.
• 각각 서로 다른 수의 단계로 분류가 가능한 변수를 포함하는 데이터에 대하여 더 많은 단계를 가지는 속성 쪽으로 정보 획득량이 편향되는 문제가 있다. 하지만 이 문제는 조건부 추론을 통해 해결이 가능하다.
• 데이터의 특성이 특정 변수에 수직/수평적으로 구분되지 못할 때 분류율이 떨어지고, 트리가 복잡해지는 문제가 발생한다. 신경망 등의 알고리즘이 여러 변수를 동시에 고려하지만 결정트리는 한 개의 변수만을 선택하기 때문에 발생하는 당연한 문제이다.
• 약간의 차이에 따라 (레코드의 개수의 약간의 차이) 트리의 모양이 많이 달라질 수 있다. 두 변수가 비슷한 수준의 정보력을 갖는다고 했을 때, 약간의 차이에 의해 다른 변수가 선택되면 이 후의 트리 구성이 크게 달라질 수 있다.

  SVM

  서포트 벡터 머신은 기계 학습의 분야 중 하나로 패턴 인식, 자료 분석을 위한 지도 학습 모델이며, 주로 분류와 회귀 분석을 위해 사용한다. 두 카테고리 중 어느 하나에 속한 데이터의 집합이 주어졌을 때, SVM 알고리즘은 주어진 데이터 집합을 바탕으로 하여 새로운 데이터가 어느 카테고리에 속할지 판단하는 비확률적 이진 선형 분류 모델을 만든다. 만들어진 분류 모델은 데이터가 사상된 공간에서 경계로 표현되는데 SVM 알고리즘은 그 중 가장 큰 폭을 가진 경계를 찾는 알고리즘이다. SVM은 선형 분류와 더불어 비선형 분류에서도 사용될 수 있다. 비선형 분류를 하기 위해서 주어진 데이터를 고차원 특징 공간으로 사상하는 작업이 필요한데, 이를 효율적으로 하기 위해 커널 트릭을 사용하기도 한다

  Logisitic regression

  로지스틱 회귀(영어: logistic regression)는 D.R.Cox가 1958년에 제안한 확률 모델로서 독립 변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는데 사용되는 통계 기법이다.로지스틱 회귀의 목적은 일반적인 회귀 분석의 목표와 동일하게 종속 변수와 독립 변수간의 관계를 구체적인 함수로 나타내어 향후 예측 모델에 사용하는 것이다. 이는 독립 변수의 선형 결합으로 종속 변수를 설명한다는 관점에서는 선형 회귀 분석과 유사하다. 하지만 로지스틱 회귀는 선형 회귀 분석과는 다르게 종속 변수가 범주형 데이터를 대상으로 하며 입력 데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나뉘기 때문에 일종의 분류 (classification) 기법으로도 볼 수 있다. 흔히 로지스틱 회귀는 종속변수가 이항형 문제(즉, 유효한 범주의 개수가 두개인 경우)를 지칭할 때 사용된다. 이외에, 두 개 이상의 범주를 가지는 문제가 대상인 경우엔 다항 로지스틱 회귀 (multinomial logistic regression) 또는 분화 로지스틱 회귀 (polytomous logistic regression)라고 하고 복수의 범주이면서 순서가 존재하면 서수 로지스틱 회귀 (ordinal logistic regression) 라고 한다. 로지스틱 회귀 분석은 의료, 통신, 데이터마이닝과 같은 다양한 분야에서 분류 및 예측을 위한 모델로서 폭넓게 사용되고 있다

  KNN

  패턴 인식에서, k-최근접 이웃 알고리즘(또는 줄여서 k-NN)은 분류나 회귀에 사용되는 비모수 방식이다. 두 경우 모두 입력이 특징 공간 내 k개의 가장 가까운 훈련 데이터로 구성되어 있다. 출력은 k-NN이 분류로 사용되었는지 또는 회귀로 사용되었는지에 따라 다르다.k-NN 분류에서 출력은 소속된 항목이다. 객체는 k개의 최근접 이웃 사이에서 가장 공통적인 항목에 할당되는 객체로 과반수 의결에 의해 분류된다(k는 양의 정수이며 통상적으로 작은 수). 만약 k = 1 이라면 객체는 단순히 하나의 최근접 이웃의 항목에 할당된다.k-NN 회귀에서 출력은 객체의 특성 값이다. 이 값은 k개의 최근접 이웃이 가진 값의 평균이다.k-NN은 함수가 오직 지역적으로 근사하고 모든 계산이 분류될 때까지 연기되는 인스턴스 기반 학습 또는 게으른 학습의 일종이다. k-NN 알고리즘은 가장 간단한 기계 학습 알고리즘에 속한다.분류와 회귀 모두 더 가까운 이웃일수록 더 먼 이웃보다 평균에 더 많이 기여하도록 이웃의 기여에 가중치를 주는 것이 유용할 수 있다. 예를 들어, 가장 흔한 가중치 스키마는 d가 이웃까지의 거리일 때 각각의 이웃에게 1/d의 가중치를 주는 것이다. 이웃은 항목(k-NN 분류의 경우)이나 객체 특성 값(k-NN 회귀의 경우)이 알려진 객체의 집합으로부터 구해진다. 이것은 명시적인 훈련 과정이 필요하지는 않지만, 알고리즘을 위한 훈련 집합이라고 생각될 수 있다.

Algorithm

Algorithm

KMN

k-평균 클러스터링 알고리즘은 클러스터링 방법 중 분할법에 속한다. 분할법은 주어진 데이터를 여러 파티션 (그룹) 으로 나누는 방법이다. 예를 들어 n개의 데이터 오브젝트를 입력받았다고 가정하자. 이 때 분할법은 입력 데이터를 n보다 작거나 같은 k개의 그룹으로 나누는데, 이 때 각 군집은 클러스터를 형성하게 된다. 다시 말해, 데이터를 한 개 이상의 데이터 오브젝트로 구성된 k개의 그룹으로 나누는 것이다. 이 때 그룹을 나누는 과정은 거리 기반의 그룹간 비유사도 (dissimilarity) 와 같은 비용 함수 (cost function) 을 최소화하는 방식으로 이루어지며, 이 과정에서 같은 그룹 내 데이터 오브젝트 끼리의 유사도는 증가하고, 다른 그룹에 있는 데이터 오브젝트와의 유사도는 감소하게 된다. k-평균 알고리즘은 각 그룹의 중심 (centroid)과 그룹 내의 데이터 오브젝트와의 거리의 제곱합을 비용 함수로 정하고, 이 함수값을 최소화하는 방향으로 각 데이터 오브젝트의 소속 그룹을 업데이트 해 줌으로써 클러스터링을 수행하게 된다.

algorithm

입력값

1. k: 클러스터 수
2. D: n 개의 데이터 오브젝트를 포함하는 집합

출력값: k 개의 클러스터

1. 데이터 오브젝트 집합 D에서 k 개의 데이터 오브젝트를 임의로 추출하고, 이 데이터 오브젝트들을 각 클러스터의 중심 (centroid) 으로 설정한다. (초기값 설정)
2. 집합 D의 각 데이터 오브젝트들에 대해 k 개의 클러스터 중심 오브젝트와의 거리를 각각 구하고, 각 데이터 오브젝트가 어느 중심점 (centroid) 와 가장 유사도가 높은지 알아낸다. 그리고 그렇게 찾아낸 중심점으로 각 데이터 오브젝트들을 할당한다.
3. 클러스터의 중심점을 다시 계산한다. 즉, 2에서 재할당된 클러스터들을 기준으로 중심점을 다시 계산한다.
4. 각 데이터 오브젝트의 소속 클러스터가 바뀌지 않을 때 까지 2, 3 과정을 반복한다.

Linear regression

선형 회귀는 선형 예측 함수를 사용해 회귀식을 모델링하며, 알려지지 않은 파라미터는 데이터로부터 추정한다. 이렇게 만들어진 회귀식을 선형 모델이라고 한다. 선형 회귀는 깊이있게 연구되고 널리 사용된 첫 번째 회귀분석 기법이다.[3] 이는 알려지지 않은 파라미터에 대해 선형 관계를 갖는 모델을 세우는 것이, 비선형 관계를 갖는 모델을 세우는 것보다 용이하기 때문이다. 값을 예측하는 것이 목적일 경우, 선형 회귀를 사용해 데이터에 적합한 예측 모형을 개발한다. 개발한 선형 회귀식을 사용해 y가 없는 x값에 대해 y를 예측하기 위해 사용할 수 있다. 종속 변수 y와 이것과 연관된 독립 변수 X1, …, Xp가 존재하는 경우에, 선형 회귀 분석을 사용해 Xj와 y의 관계를 정량화할 수 있다. Xj는 y와 전혀 관계가 없을 수도 있고, 추가적인 정보를 제공하는 변수일 수도 있다. 일반적으로 최소제곱법(least square method)을 사용해 선형 회귀 모델을 세운다. 최소제곱법 외에 다른 기법으로도 선형 회귀 모델을 세울 수 있다. 손실 함수(loss fuction)를 최소화 하는 방식으로 선형 회귀 모델을 세울 수도 있다. 최소제곱법은 선형 회귀 모델 뿐 아니라, 비선형 회귀 모델에도 적용할 수 있다. 최소제곱법과 선형 회귀는 가깝게 연관되어 있지만, 그렇다고 해서 동의어는 아니다.

Logistic Regression vs Decision Trees vs SVM

Logistic Regression

Logistic Regression Pros:

• Convenient probability scores for observations
• Efficient implementations available across tools
• Multi-collinearity is not really an issue and can be countered with L2 regularization to an extent
• Wide spread industry comfort for logistic regression solutions [ oh that’s important too!]

Logistic Regression Cons:

• Doesn’t perform well when feature space is too large
• Doesn’t handle large number of categorical features/variables well
• Relies on transformations for non-linear features
• Relies on entire data

Decision Tree

Decision Trees Pros:

• Intuitive Decision Rules
• Can handle non-linear features
• Take into account variable interactions

Decision Trees Cons:

• Highly biased to training set [Random Forests to your rescue]
• No ranking score as direct result

SVM

SVM Pros:

• Can handle large feature space
• Can handle non-linear feature interactions
• Do not rely on entire data

SVM Cons:

• Not very efficient with large number of observations
• It can be tricky to find appropriate kernel sometimes

Conclusion

• Always start with logistic regression, if nothing then to use the performance as baseline
• See if decision trees (Random Forests) provide significant improvement. Even if you do not end up using the resultant model, you can use random forest results to remove noisy variables
• Go for SVM if you have large number of features and number of observations are not a limitation for available resources and time

Overfitting & Regularization

overfiting

Prunning

Prunning 아래와 같이 두가지가 있다

• Pre-pruning that stop growing the tree earlier, before it perfectly classifies the training set.
• Post-pruning that allows the tree to perfectly classify the training set, and then post prune the tree.

supervised vs unsupervised learning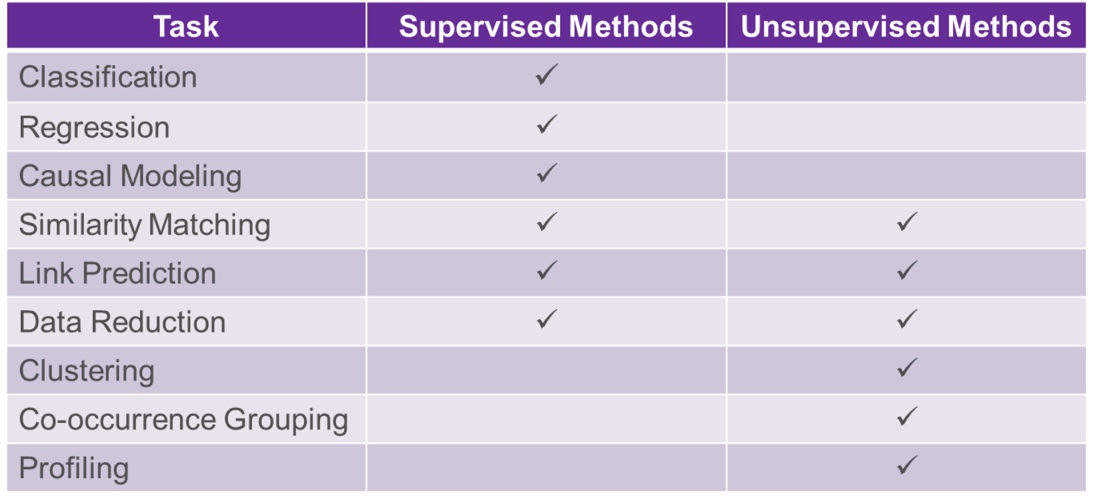

Information Gain

• Entropy = $-p_1log(p_1) - p_2log(p_2) -p_3log(p_3) - ⋯⋯$ → example들의 집합에서의 혼합성(impurity)을 나타냄
• Information Gain = IG(parent, children) = entropy(parent) - $(p(c_1) × entropy(c_1) + p(c_2) × entropy(c_2) + ⋯)$ → 지정된 속성이 얼마나 잘 training example들간을 구분하는가에 대한 수치. 특정 속성을 기준으로 example들을 구분하게될 때, ‘감소되는 entropy의 양’을 의미한다.

  분류나무는 구분 뒤 각 영역의 순도(homogeneity)가 증가, 불순도(impurity) 혹은 불확실성(uncertainty)이 최대한 감소하도록 하는 방향으로 학습을 진행합니다. 순도가 증가/불확실성이 감소하는 걸 두고 정보이론에서는 정보획득(information gain)이라고 합니다.

• IG

Evaluation

distance

Euclidean Distance

p = $(p_1, p_2,..., p_n)$ q = $(q_1, q_2,..., q_n)$ 일때 |p - q| = |q - p| = $\sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2 + (p_3 - q_3)^2 + ⋯⋯ + (p_n - q_n)^2} \$

Manhatten Distance

p = $(p_1, p_2,..., p_n)$ q = $(q_1, q_2,..., q_n)$ 일때 $d_1(p,q)$ = $|p-q|_1$ = $\sum_{i=1}^n |p_i-q_i|$

Cosine Distance

$d_{cosine}(X,Y)$ = 1- $XY \over {|X|^2 |Y|^2}$ $D_c$ = 1 - $S_c$ where $D_c$ is the cosine distance and $S_c$ is the cosine similarity similarity = $cos(\theta)$ = ${A \cdot B \over |A| |B|}$ = $\frac{ \sum\limits_{i=1}^{n}{A_i \times B_i} }{ \sqrt{\sum\limits_{i=1}^{n}{(A_i)^2}} \times \sqrt{\sum\limits_{i=1}^{n}{(B_i)^2}} }$

jaccard Distance

J(A,B) = 1- $|A ∩ B| \over |A ∪ B|$ = 1- $|A ∩ B| \over |A| + |B| - |A ∩ B|$

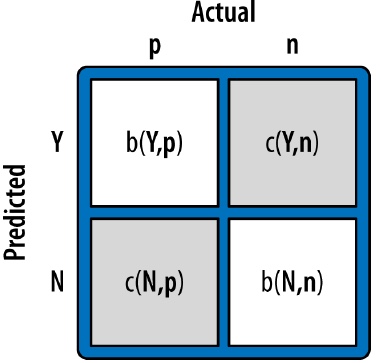
confusion matrix

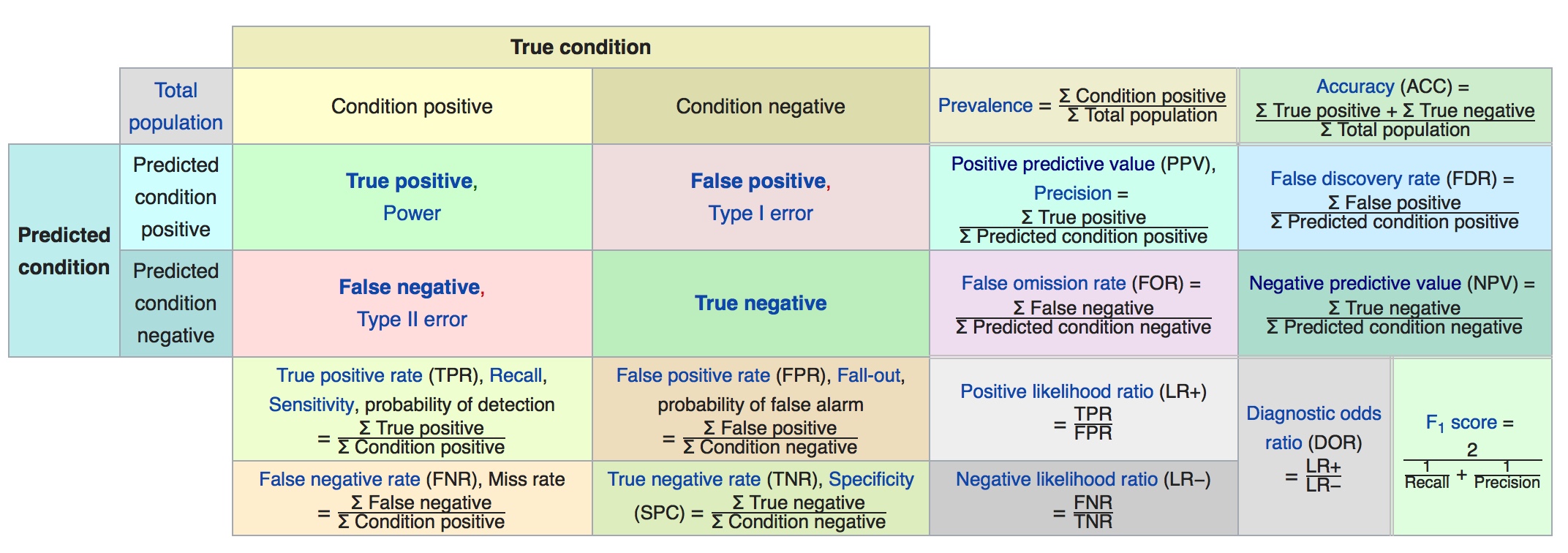
Other Evaluation Metrics

• Precision = $tp \over {tp + fp}$
• Recall= $tp \over {tp + fn}$
• F−measure = 2 × ${Precision × Recall} \over {Precision + Recall}$

Expected profit

cost-benefit matrix

ROC Graphs and Curves

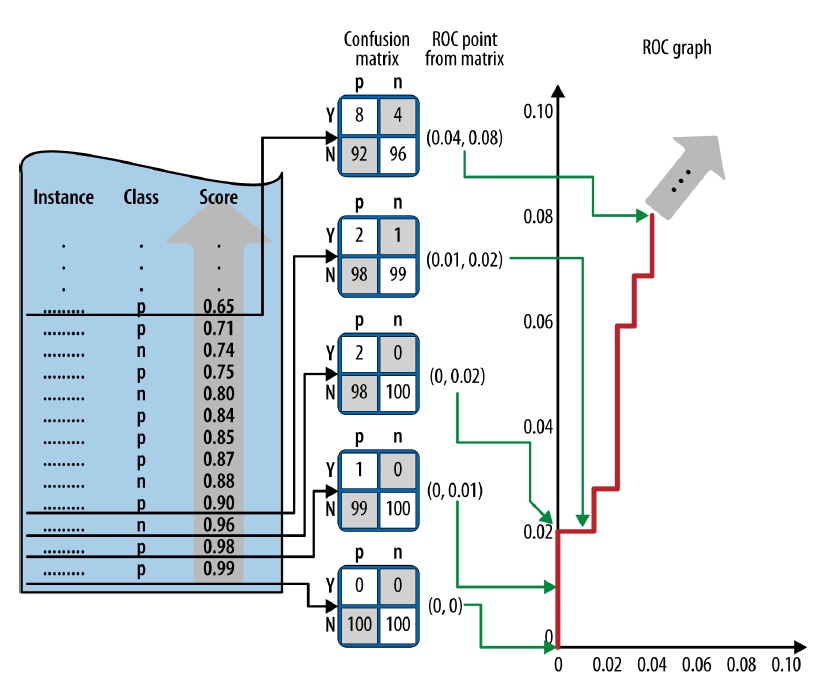
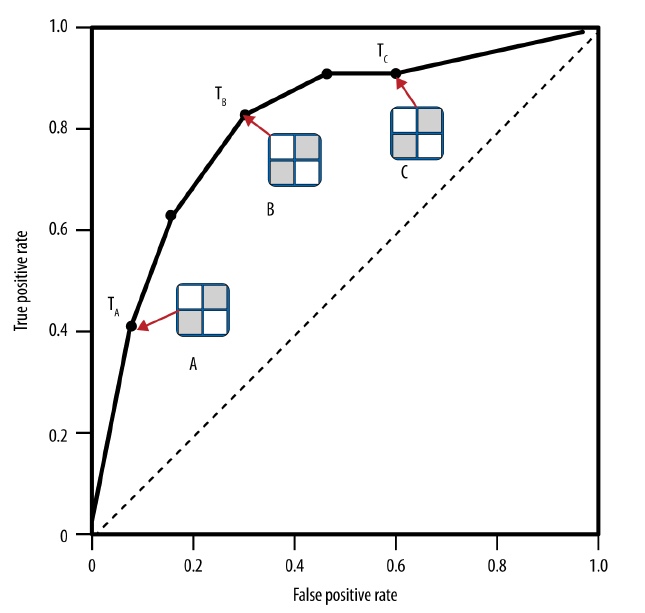
• ROC graphs decouple classifier performance from the conditions under which the classifiers will be used
• ROC graphs are independent of the class proportions as well as the costs and benefits
• Not the most intuitive visualization for many business stakeholders

Algorithm

• Sort the test set by the model predictions
• Start with cutoff = max (prediction)
• Decrease cutoff, after each step count the number of true positives TP (positives with prediction above the cutoff) and false positives FP (negatives above the cutoff)
• Calculate TP rate (TP/P) and FP (FP/N) rate
• Plot current number of TP/P as a function of current FP/N

  AUC

• ROC curve 구글님은 아래처럼 말해주고 있다

  다양한 분류 임계값에서 참긍정률과 거짓긍정률이 이루는 곡선입니다. ROC 곡선은 다양한 분류 임계값의 TPR 및 FPR을 나타냅니다. 분류 임계값을 낮추면 더 많은 항목이 양성으로 분류되므로 거짓양성과 참양성이 모두 증가합니다.

• AUC 또 구글님의 말을 적어보면

  가능한 모든 분류 임계값을 고려하는 평가 측정항목입니다. AUC(ROC 곡선 아래 영역)는 무작위로 선택한 긍정 예가 실제로 긍정일 가능성이 무작위로 선택한 부정 예가 긍정일 가능성보다 높다고 분류자가 신뢰할 확률입니다.

• link

  Cumulative Response curve

• Percentage of positive correctly classified (y-axis) vs the percentage of the population that is tangled (x-axis)
• y = x : random performance
• Any classifier above the diagonal is providing some advantage

link

Lift Curve

• The lift of a classifier represents the advantage it provides over random guessing.
• lift = ${TP rate(x)} \over x$

참고자료

• https://ko.wikipedia.org/wiki/결정_트리_학습법
• https://ko.m.wikipedia.org/wiki/서포트_벡터_머신
• http://en.wikipedia.org
• http://ko.wikipedia.org
• http://www.saedsayad.com/decision_tree_overfitting.htm
• https://developers.google.com/machine-learning/crash-course/classification/roc-and-auc?hl=ko
• https://www.u-cursos.cl/ingenieria/2017/1/IN5528/1/material_docente/bajar?id_material=1752815
• http://euriion.com/?p=548
• https://www.edvancer.in/logistic-regression-vs-decision-trees-vs-svm-part2/
• http://frontjang.info/entry/Entropy%EC%99%80-Information-Gain
• https://ratsgo.github.io/machine%20learning/2017/03/26/tree/