Over-fitting the data

알고 있는 데이터에 대해서는 아주 완벽하게 분류할 수 있으나 비슷한 것들에 대해서는 잘 모르게 되는 상태 아래 그림처럼 부드럽게 분류를 해야 하는데 현재 데이터에 집중하다보니 현재 데이터에만 잘 맞고 일반적인 데이터에 안맞는 상태 이렇게 되면 기껏 만들어서 일부데이터에만 맞게 개고생하게 되니 일반화를 해줘야함

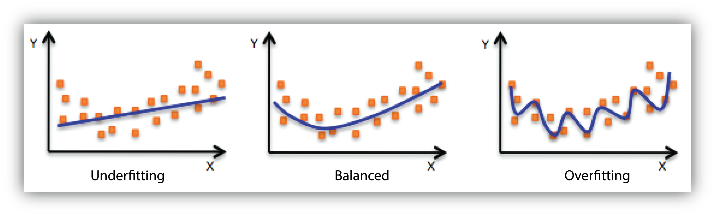
Over-fitting

• 결국 data mining 방법론들은 모두 overfitting할 가능성이 존재함 그리고 overfitting을 제거할 수 있는 silver bullet은 없다. 이를 위해 해결하는 방법은 여기 일반론적인 내용이 있음
• Pattern을 학습해서 다른곳에도 써먹을려고 했던 모델이였는데 데이터를 외워버리니 답이 없다. 하라는 공부는 안하고
• 이 슬라이드 주제와는 좀 다른 문제이긴 한데 underfitting 과 good fit 그리고 overfitting에 대한 엄밀한 정의는 없는 듯 하다 애정남이 필요해 대략적으로 변곡점에서 찾는것 같긴 한데 애매하다.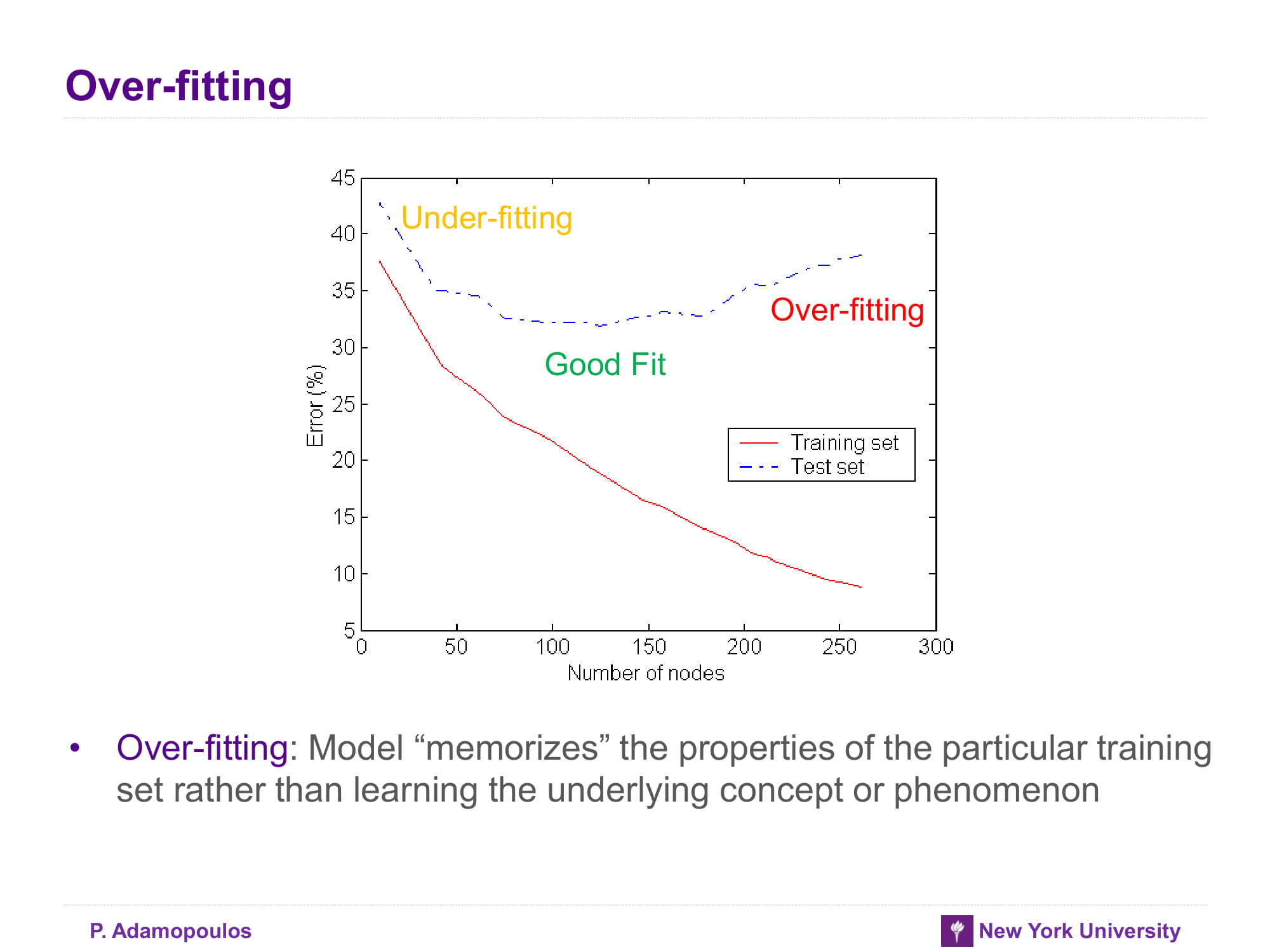

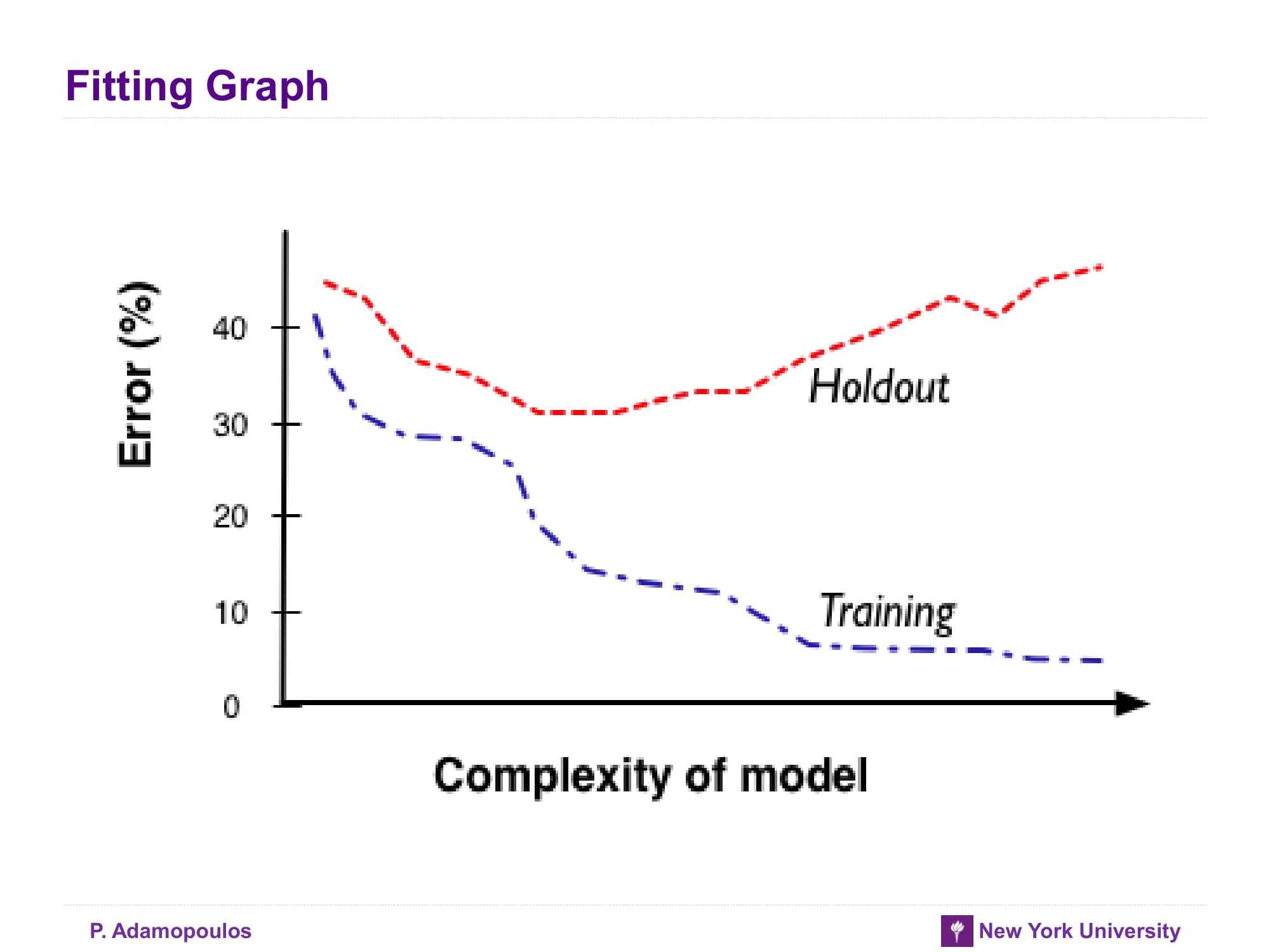
Fitting Graph

모델이 복잡해질 수록 현재 학습데이터에는 잘 맞게 되지만 실제 다른데이터에는 맞지 않게 된다. 생각해 보면 특정 데이터를 잘 묘사하기 위해서는 그 데이터만 있는 특성까지 잘 파악해서 분류할 수 있어야 하는데 다른 데이터들에 그 특성이 없으면 당연히 잘 안맞게 된다.

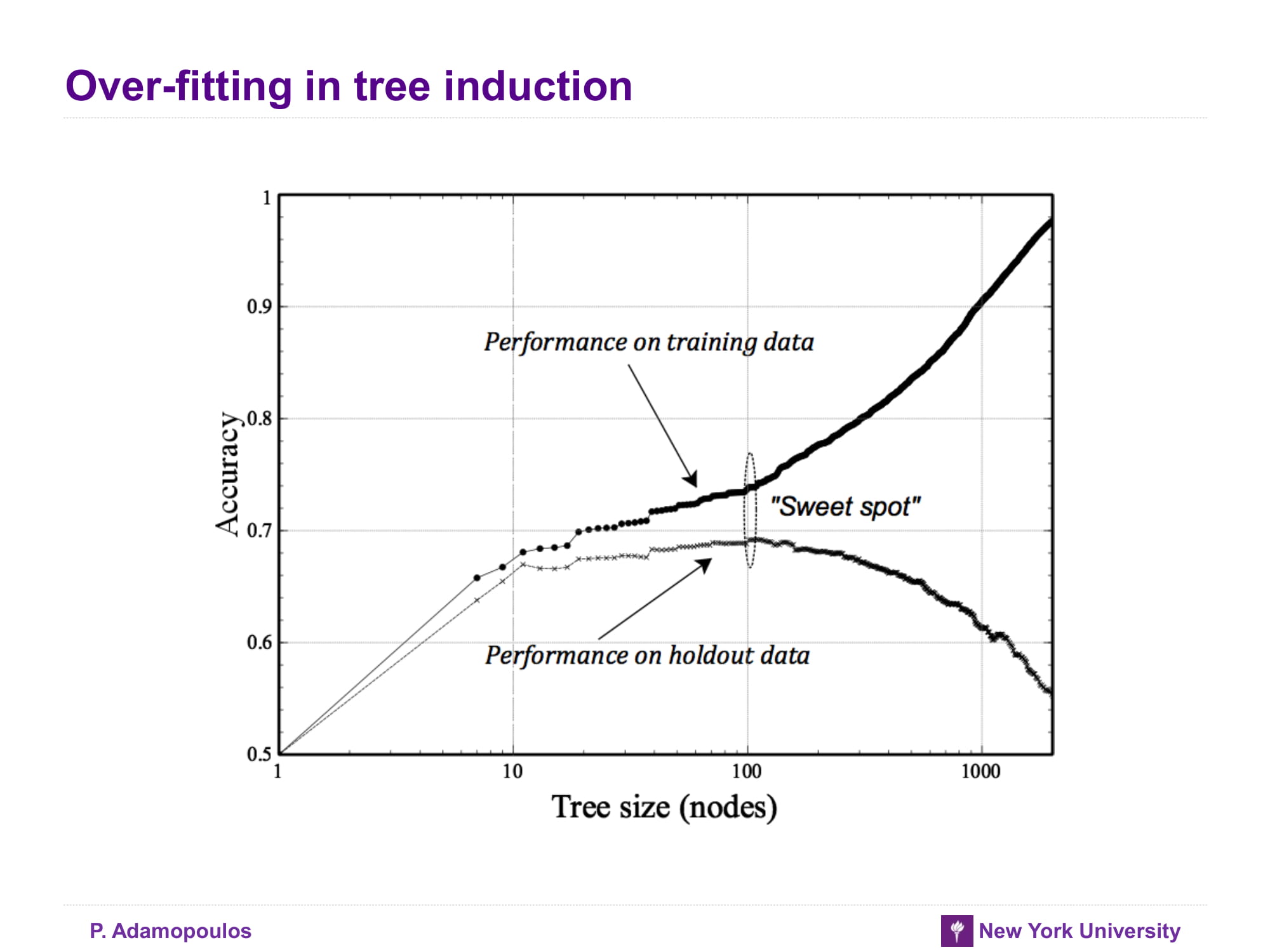
Over-fitting in tree induction

그래서 학습데이터에서 학습률이 상승하면서 test data에서 학습률이 감소하는 그 지점에서 학습을 멈추면 좋다라고는 하지만 정말 뜬구름 잡는 말인듯 산은 산이고 물은 물이다 일단 그런 지점을 sweet spot이라고 한다고 한다

Over-fitting in linear

아래로 가면 갈 수록 모델이 복잡해진다. 결국 overfitting이 발생할 것이다.

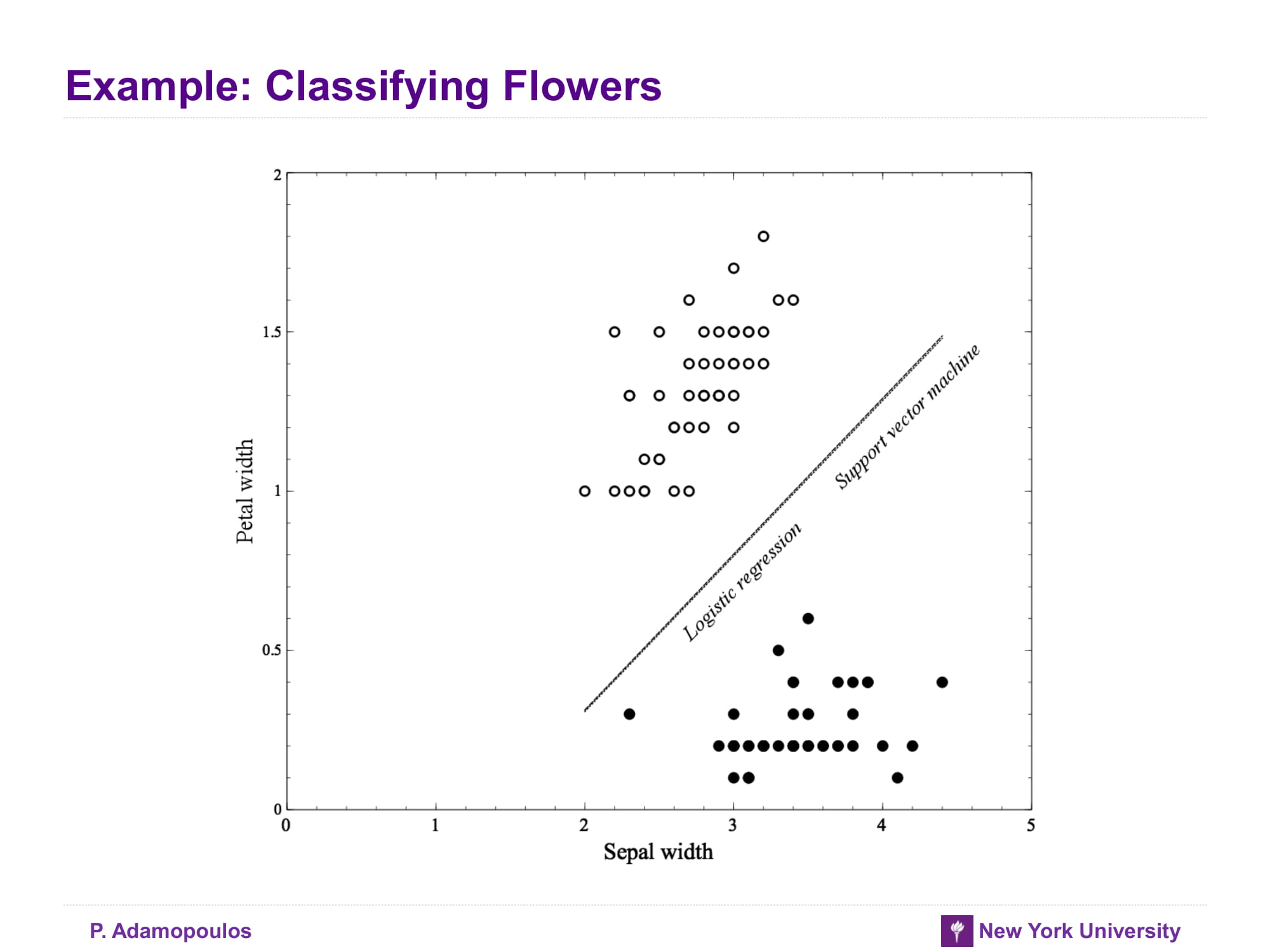
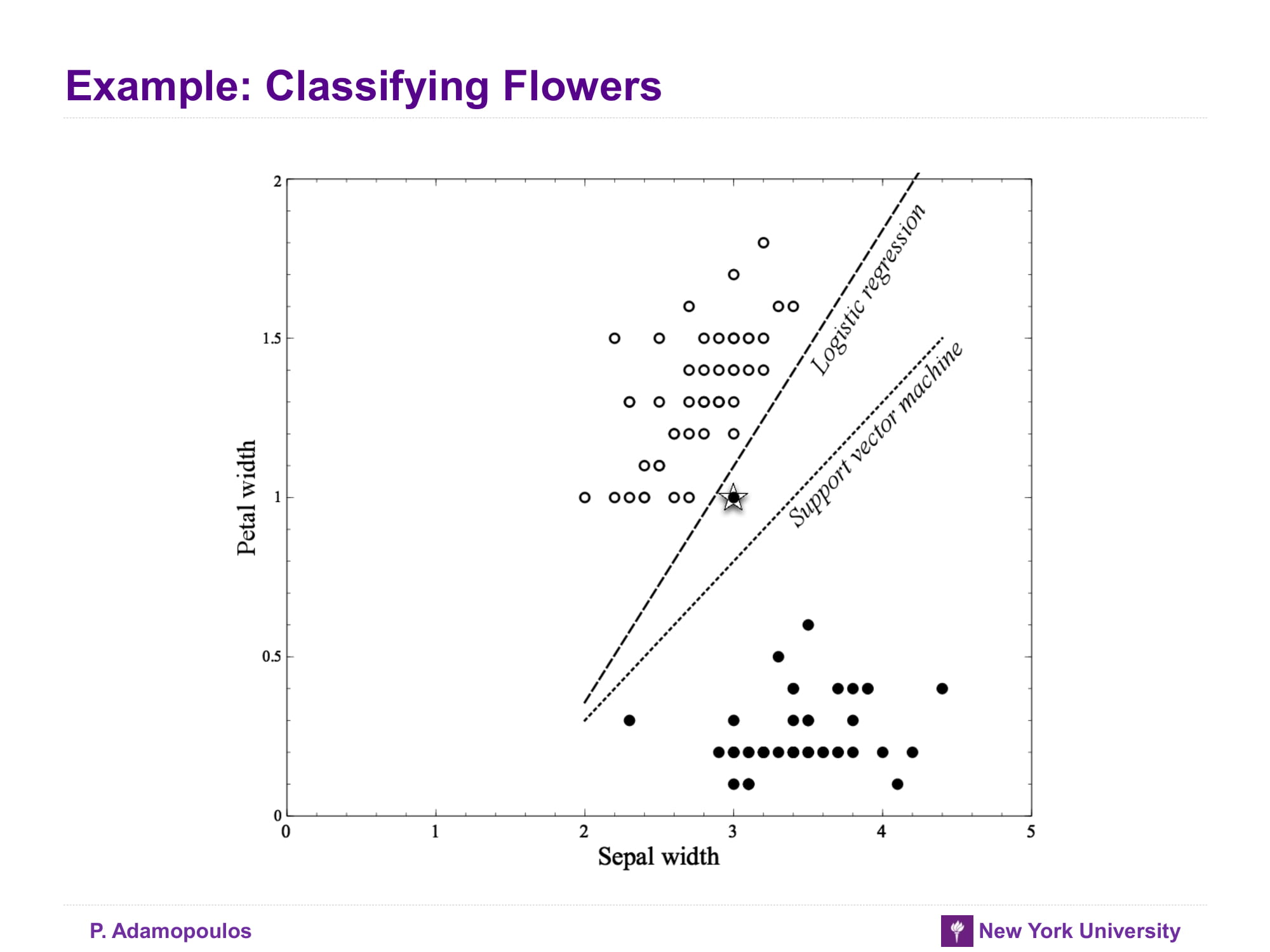
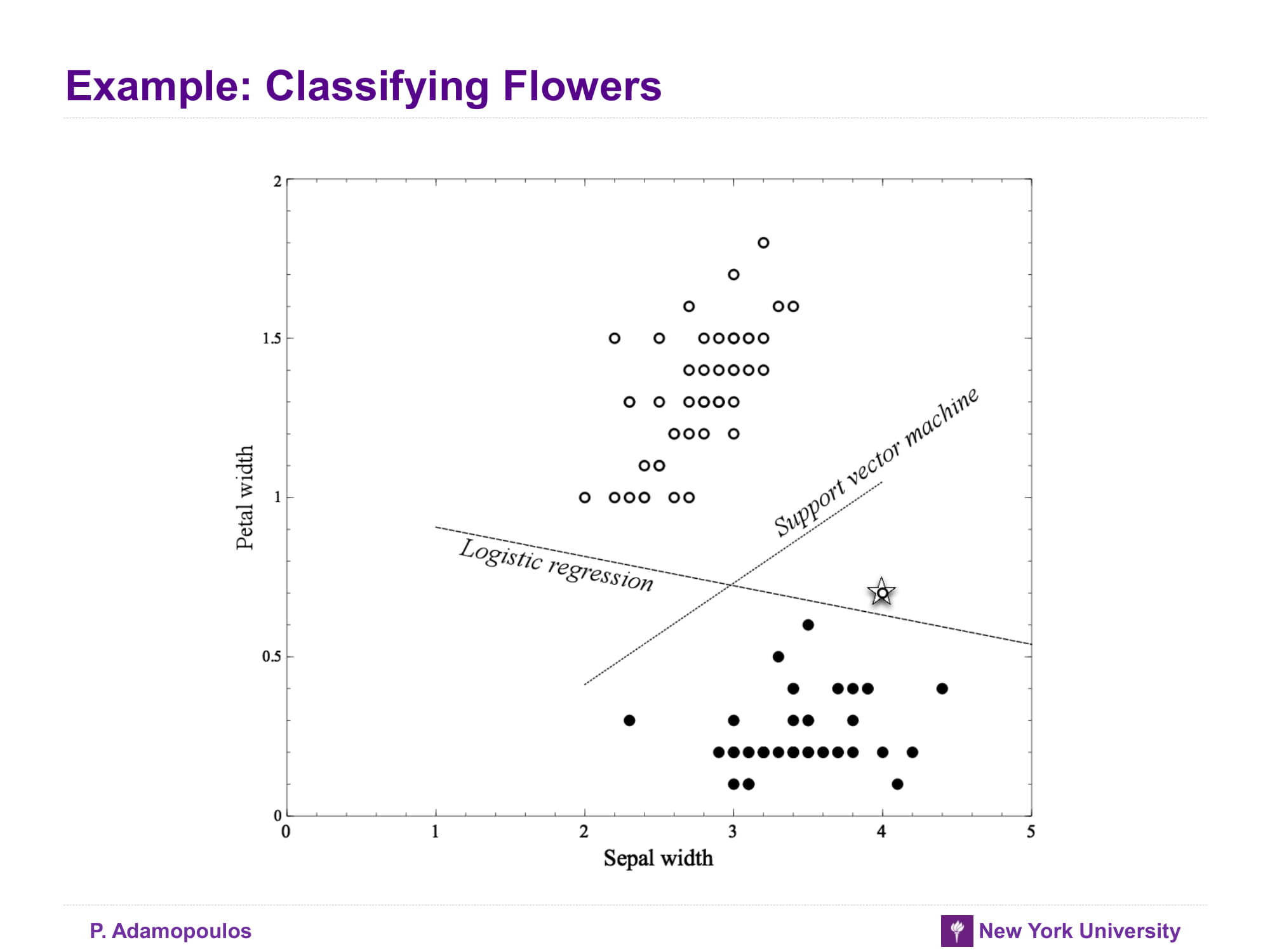
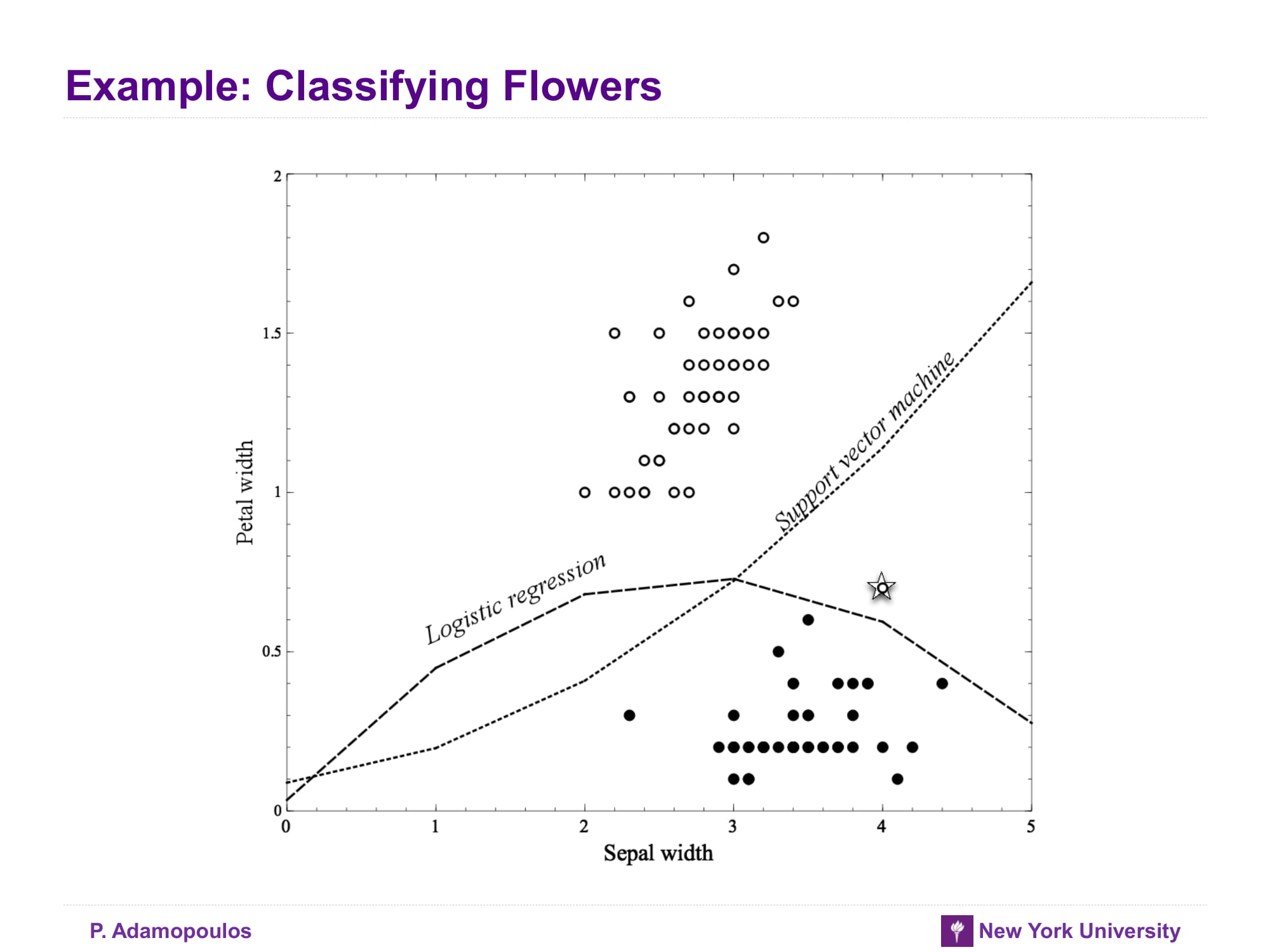
Example: Classifying Flowers

아래 그래프들는 attribute가 늘어날 수록 overfitting이 된다는 것을 보여주며 logistic regression이 SVM보다 overfitting일어날 가능성이 높다고 말하고 있다 잠깐 왜 logisistic regression이 SVM보다 overfitting이 잘 일어나는거지? 일단 교과서에서는 outlier에 logitstic regression이 좀 더 취약하다고 한다. 잠시 logistic regression 을 수식으로 나타내면 아래와 같다

• $σ(t)$ = $1 \over e^-t(x)$ where $t(x) = α_0 + α_1x_1 + α_2x_2 + a_3x_3+ ...$

이런 상황이니 새로운 값이 들어오면 변화가 큰 것 같다

Avoiding Over-fitting

overfitting이 문제인 것은 이제 알았으니 어떤 방법으로 이 어려움을 피해갈지 생각해보자

Tree-induction

• decision tree는 이미 배운 것과 같이 pruning을 수행하면 된다
• 크게 pre-pruning과 post-pruning이 있다
  • pre-pruning : to stop growing the tree before it gets too complex,
  • post-pruning: to grow the tree until it is too large, then “prune” it back, reducing its size (and thereby its complexity).

Linear model

• feature selection wikipedia의 내용을 보면 아래와 같다

In machine learning and statistics, feature selection, also known as variable selection, attribute selection or variable subset selection, is the process of selecting a subset of relevant features (variables, predictors) for use in model construction.

feature selection이 어떤식으로 Generalization에 기여하는지 찾아보면 아래와 같다 (원문은 여기에서 확인가능 )

Feature selection methods can be used to identify and remove unneeded, irrelevant and redundant attributes from data that do not contribute to the accuracy of a predictive model or may in fact decrease the accuracy of the model. Fewer attributes is desirable because it reduces the complexity of the model, and a simpler model is simpler to understand and explain.

결국 complexity를 줄여서 일반화를 시킬 수 있다는 말이다.

• Regularization 교과서 소제목에 * 가 있는게 심히 신경쓰인다
  • $fit(x,w)$ : 특정 testset에 얼마나 잘 맞는지 보여주는 함수다 따라서 overfitting을 고려하지 않으면 $argmax_w(fit(w,x))$를 찾는게 목표다
  • $penalty(w)$ : complexity가 커질수록 커지는 함수 complexity가 커질수록 overfitting이 커지므로 해당 함수가 커질 수록 overfitting이 심하다고 할 수 있다
  • $argmax_w(fit(w,x) - λ \cdot penalty(w))$ : linear model에서 Regularization을 하기위해서 위 식을 계산하면 된다

그리고 L1-norm이 feature selection을 할 수 있는 이유는 책에 다음과 같이 나와 있다

For reasons that are quite technical, L1-regularization ends up zeroing out many coefficients. Since these coefficients are the multiplicative weights on the features, L1-regularization effectively performs an automatic form of feature selection.

결국 불필요한 feature들을 0으로 보내버리니 feature selection이 되는 의미 교과서에는 수식을 거의 안쓰고 설명을 하는 경우가 많아서 애매한 경우가 좀 있다 그래서 추가적으로 Regularization에 대해서는 아래 글을 보면 될 것 같다 Andrew Ng 교수님 만세 ㅜㅜ ML4-Regularization

Regularization

Need for holdout evaluation

이유는 뭐 결국 검증하기 위해서는 testset이 필요하다. overfitting 확인해 봐야지

Holdout validation

인터넷에 찾아보니 이런 글이 있다

The holdout method is the simplest kind of cross validation. The data set is separated into two sets, called the training set and the testing set. The advantage of this method is that it is usually preferable to the residual method and takes no longer to compute. However, its evaluation can have a high variance. The evaluation may depend heavily on which data points end up in the training set and which end up in the test set, and thus the evaluation may be significantly different depending on how the division is made.

결국 test set과 training set을 나눌 때 어떤 식으로 나눌지에 따라 많은 변화가 있을 수 있다. 이렇게 되면 test set과 training set을 나누어도 모델에 대한 신뢰가 떨어질 것 같은데.. 이점을 cross-validation으로 해결할 수 있을 것 같다

Cross-Validation

데이터를 여러 덩어리로 나누고 각각 덩어리들을 training set / test set으로 나누고 그결과를 평균해서 구한다. 자세한 내용은 아래 글을 참고할 것

K-fold cross validation is one way to improve over the holdout method. The data set is divided into k subsets, and the holdout method is repeated k times. Each time, one of the k subsets is used as the test set and the other k-1 subsets are put together to form a training set. Then the average error across all k trials is computed. The advantage of this method is that it matters less how the data gets divided. Every data point gets to be in a test set exactly once, and gets to be in a training set k-1 times. The variance of the resulting estimate is reduced as k is increased. The disadvantage of this method is that the training algorithm has to be rerun from scratch k times, which means it takes k times as much computation to make an evaluation. A variant of this method is to randomly divide the data into a test and training set k different times. The advantage of doing this is that you can independently choose how large each test set is and how many trials you average over.

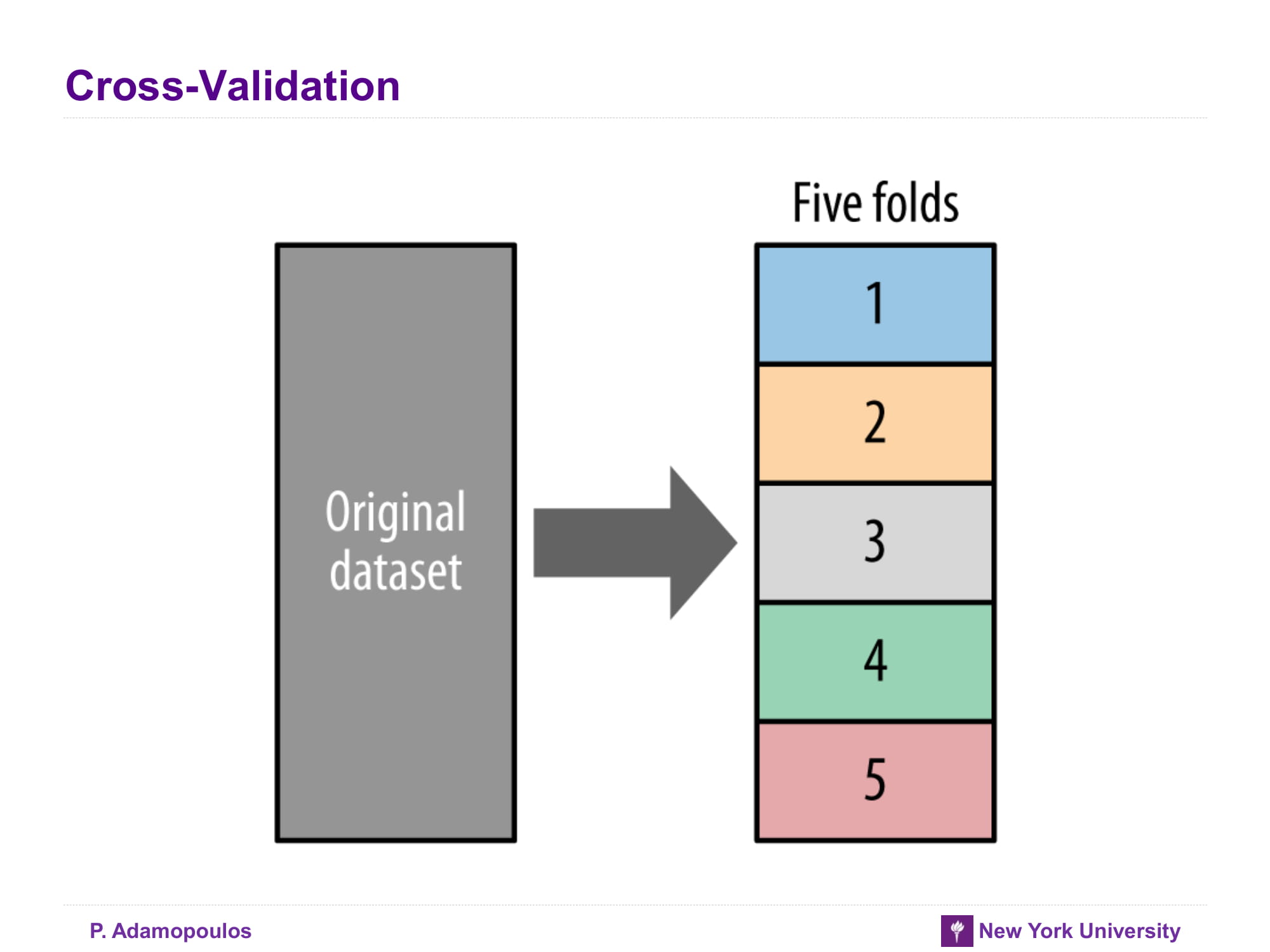
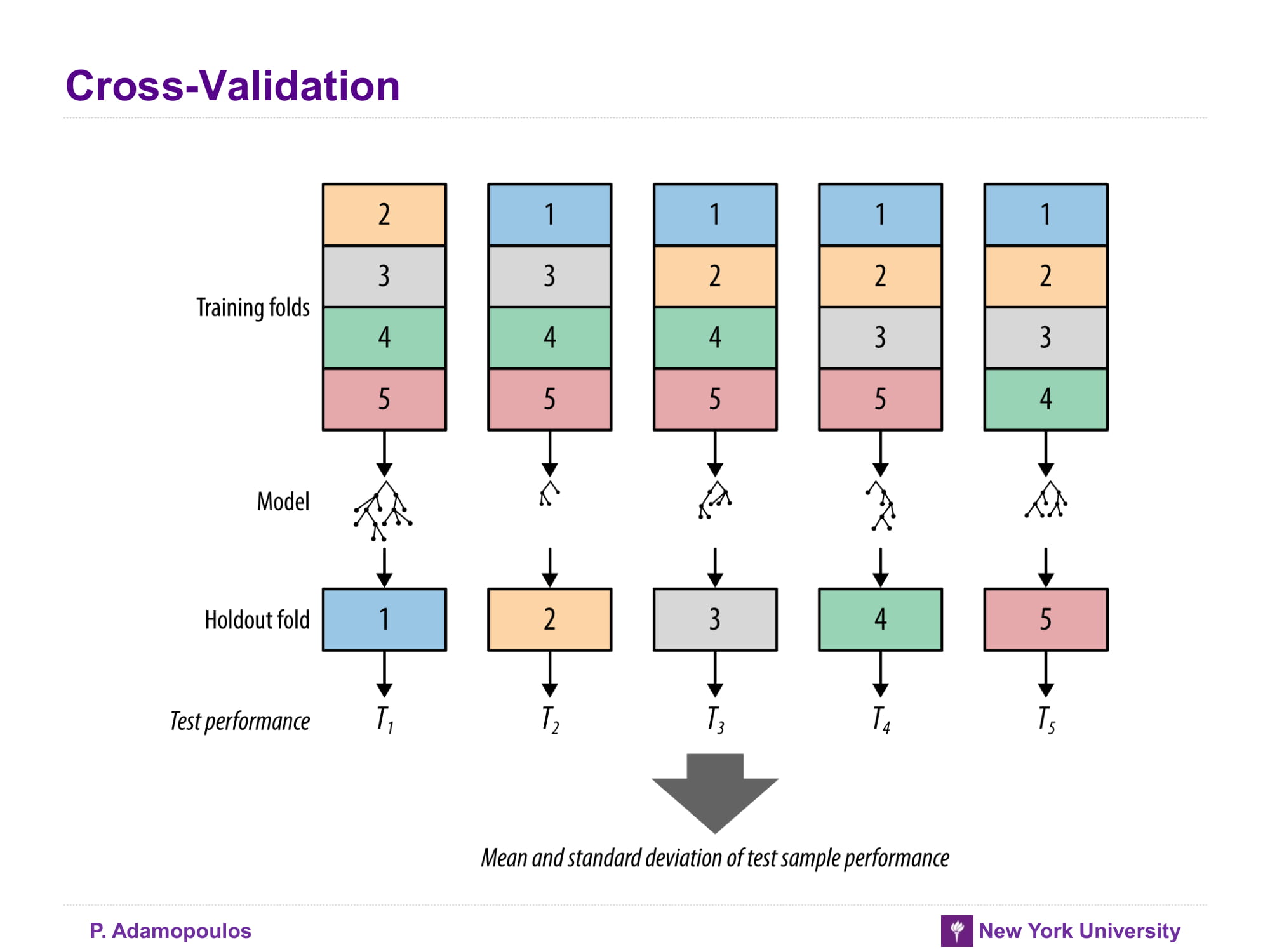
From Holdout Evaluation to Cross-Validation

위 슬라이드와 내용 동일 추가로 데이터가 작을 때 유용하다고 한다.

Nested Cross-Validation

모델뿐만 아니라 hyperparameter들도 최적화가 필요할 때 사용하는 방법

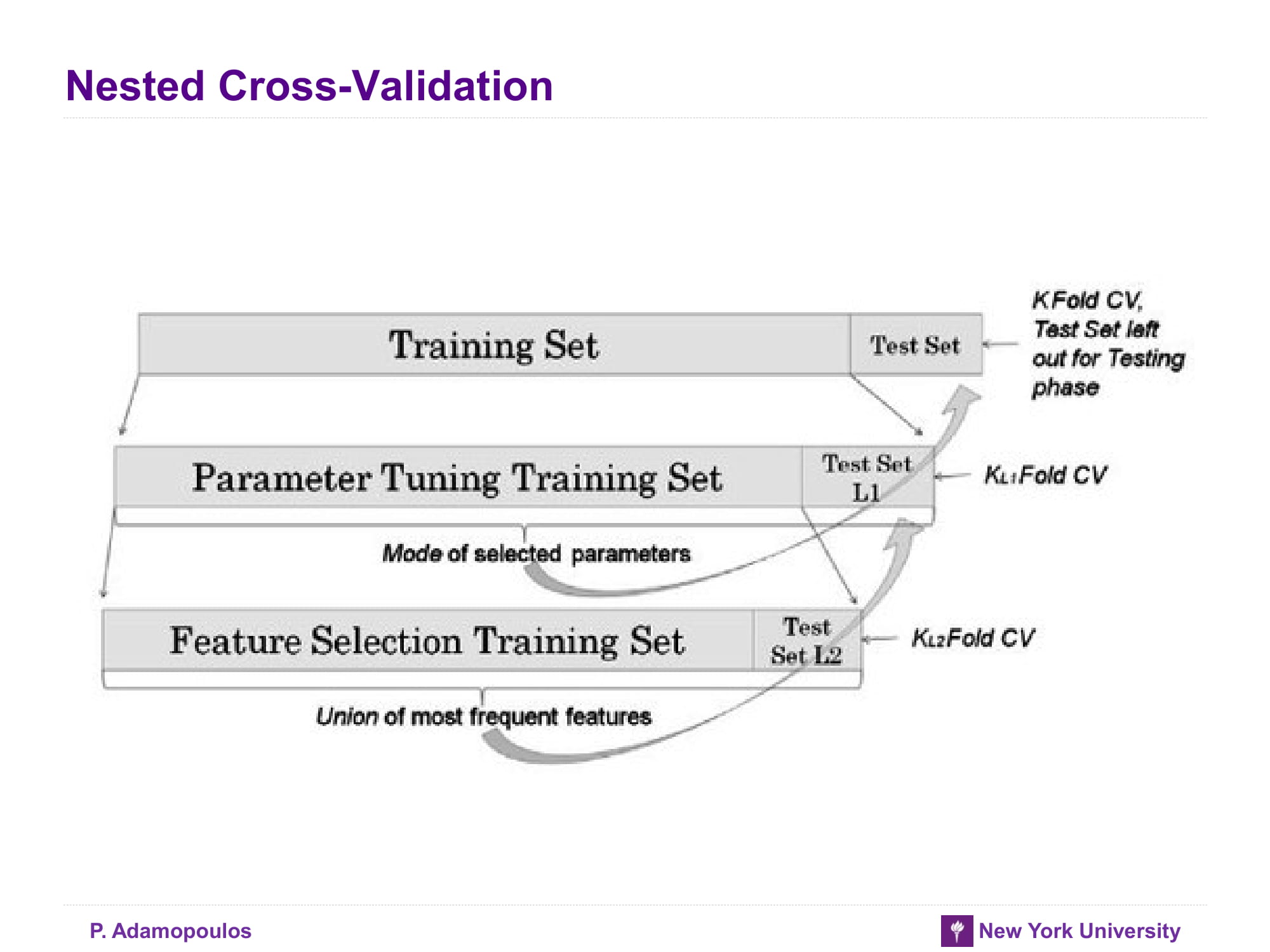
Generalization Performance

너무 당연한 이야기라 할 말이 음슴

Logistic Regression vs Tree Induction

각 algorithm의 특징을 적어주고 있다 실제 해당 algorithm들을 비교한 논문을 보면 아래 슬라이드 처럼 나온다.

Learning Curves

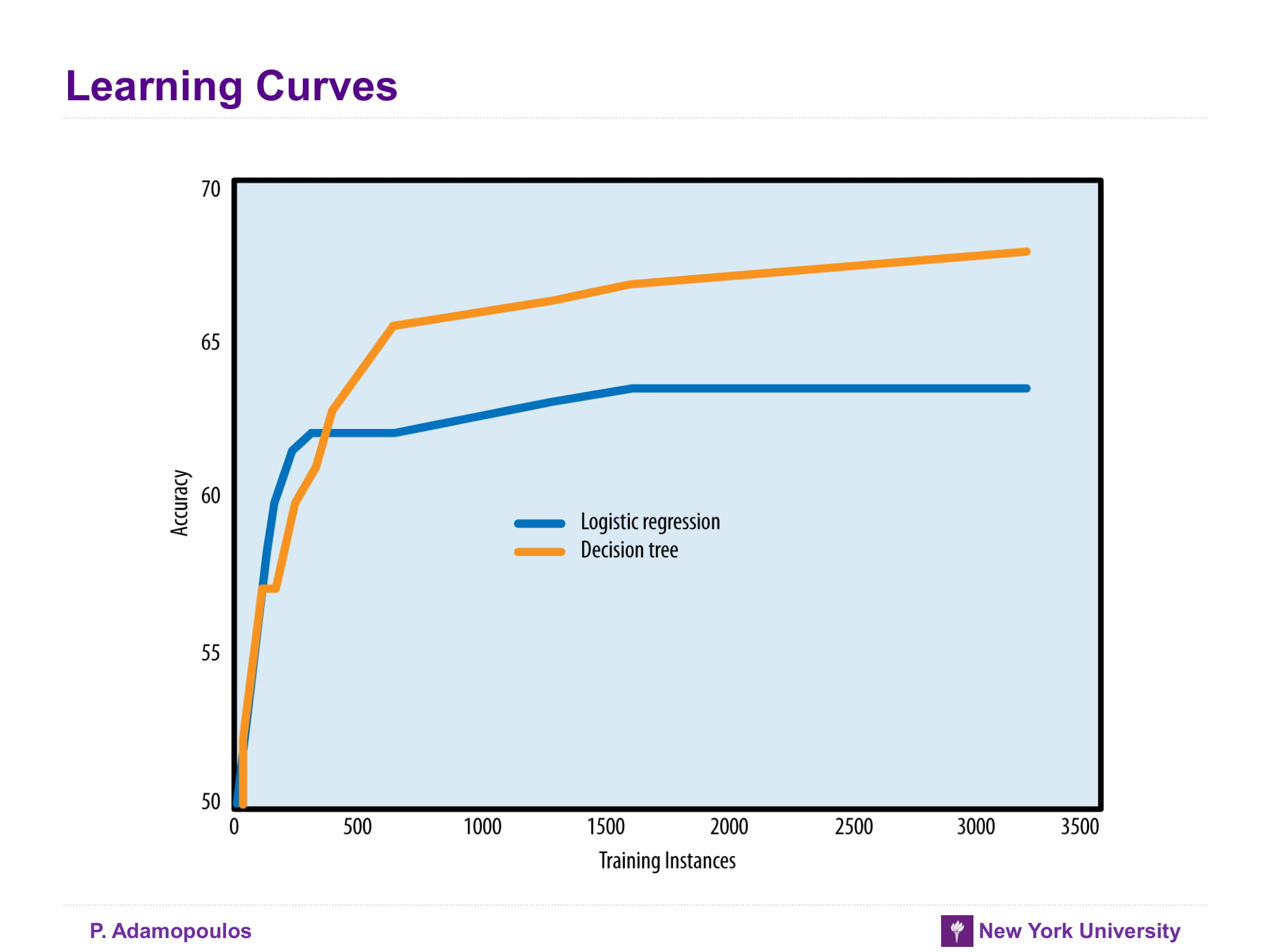
Learning curves vs Fitting graphs

참고자료

• https://docs.aws.amazon.com/ko_kr/machine-learning/latest/dg/model-fit-underfitting-vs-overfitting.html
• https://machinelearningmastery.com/an-introduction-to-feature-selection/
• https://www.cs.cmu.edu/~schneide/tut5/node42.html
• https://en.wikipedia.org/wiki/Main_Page
• Data Science for Business by Foster Provost and Tom Fawcett